Problema Hadwiger-Nelson rezolvată, după 70 de ani, de un biogerontolog

Problema Hadwiger-Nelson, rămasă nerezolvată timp de 70 de ani, şi care i-a preocupat pe marii matematicieni ai lumii, fără ca cineva să fi ajuns la un rezultat viabil, pare a-şi fi găsit, în sfârşit, soluţia. Aceasta nu a venit din partea specialiştilor în matematică, ci de la un om de ştiinţă englez – Aubrey de Grey – informatician şi autodidact în biogerontologie – un domeniu al biologiei care se ocupă cu studiul cauzelor îmbătrânirii şi al consecinţelor asupra organismului.

Aubrey de Grey a publicat soluţia sa pentru problema de matematică Hadwiger-Nelson, pe ArXiv, o bază de date cu lucrări prepublicate, din domenii ştiinţifice diverse – matematică, fizică, biologie, calcul numeric, geostiinte etc.- gestionată de Laboratorul Naţional Los Alamos (LANL), SUA, una dintre cele mai mari instituţii ştiinţifice şi tehnologice din lume, cu un buget anual de peste două miliarde de dolari.

Până la momentul actual, numărul lucrărilor ştiinţifice publicate pe ArXiv este estimat la circa un milion, baza de date menţionată putând fi accesată şi prin Astrophysics Data System (ADS), bază de date creată şi susţinută de Universitatea Harvard, şi pe INSPIRE-HELP, bază de date coordonată de Universitatea Stanford (California).

Informaticianul şi biogerontologul Aubrey de Grey este şi organizator al campionatelor mondiale şi campion al cunoscutul joc “Othello” sau “Reversi”, context în care a aprofundat teoria grafurilor, acest fapt ajutându-l în găsirea unei soluţii la problema Hadwiger-Nelson, după cum el însuşi mărturisea. “Othello”/”Reversi” este un joc care se desfăşoară pe o tablă asemănătoare cu cea de şah, de 8×8, împărţită în pătrate, cu 64 de discuri, albe pe o parte şi negre pe cealaltă, la care participă doi jucători sau două echipe, bazat pe strategii combinatorii. Cei care îl practică îl promovează cu sloganul: “Îţi trebuie un minut să înveţi acest joc şi o viaţă ca să ajungi maestru”.

Problema Hadwiger-Nelson şi soluţia lui Aubrey de Grey

Problema Hadwiger-Nelson îşi trage denumirea de la cei care au propus-o, în 1950. Hugo Hadwiger este un matematician elveţian, cunoscut prin teoria care îi poartă numele, din geometria integrală, şi prin contribuţiile sale la ameliorarea “maşinii Enigma” (NEMA), folosită la criptarea şi decriptarea mesajelor secrete, iar Edward Nelson este matematician american, cu lucrări remarcabile în domeniul fizicii matematice şi în logica matematică.

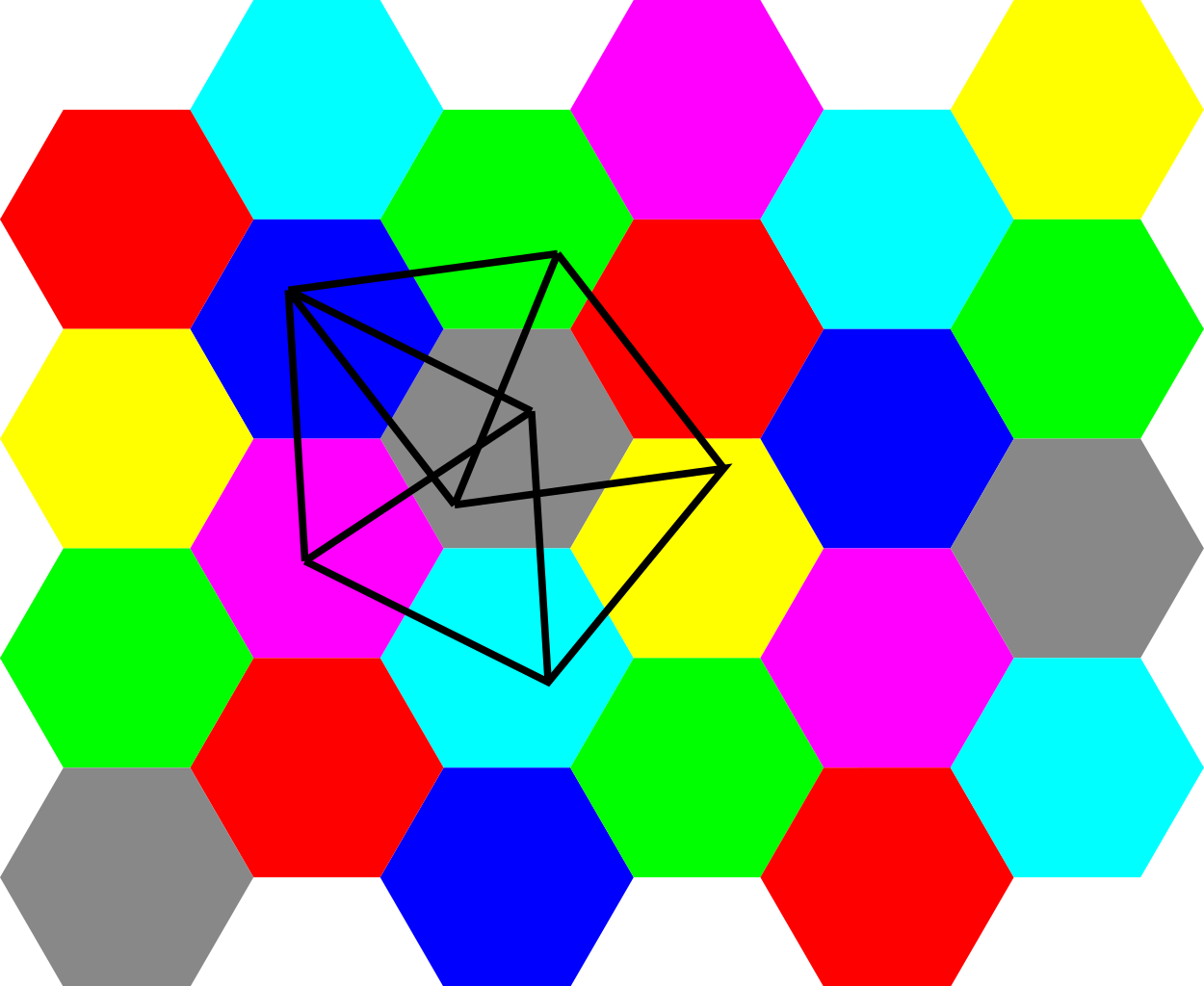
Problema Hadwiger-Nelson constă în a determina numărul minim de culori necesare pentru a colora un plan (suprafaţă plană nelimitată), de aşa manieră încât două puncte, reprezentate pe un astfel de plan, cu conexiuni potenţial infinite, să nu aibă aceeaşi culoare.

Altfel spus, dacă ne-am imagina un plan cu un număr de puncte diferite împrăştiate pe această suprafaţă, conectate prin linii de dimensiuni egale trase între ele şi fiecare punct ar fi colorat, de câte culori ar fi nevoie ca două puncte conectate să nu aibă aceeaşi culoare? Este problema care a rămas nerezolvată timp de şapte decenii şi căreia Aubrey de Grey i-a găsit o soluţie.

Valorificând teoria grafurilor (un graf fiind o mulţime de obiecte/noduri, legate printr-o mulţime de muchii) şi apelând la control computerizat, Aubrey de Grey a ajuns la concluzia că este nevoie de minimum cinci culori – “The Chromatic Number of the Plane is at least 5”, precizează informaticianul pe ArXiv, unde a publicat rezultatul calculului său şi în care mai subliniază că, pentru a colora un plan după regulile problemei, nu sunt suficiente patru culori.

Un graf este un model matematic, care permite vizualizarea şi stabilirea unei ordini logice între elementele care compun un sistem şi este format din puncte (vârfuri) legate prin segmente. În grafurile simple, pentru a se respecta condiţia din problema Hadwiger-Nelson, ca vârfurile legate printr-un segment să fie colorate diferit, ar fi nevoie de minimum două sau trei culori, iar în grafurile complexe, de minimum patru culori.

Înainte de Aubrei de Grey, şi alţi matematicieni celebri au căutat soluţii la problema Hadwiger-Nelson, precum Paul Erdos, care a ajuns la concluzia că răspunsul este cuprins între minimum patru şi maximum şapte culori, dar fără a se ajunge la o demonstratie clară.

Când Aubrei de Grey şi-a publicat soluţia la problema Hadwiger-Nelson, acesta mărturisea că “a fost extraordinar de norocos, pentru că nu se întâmplă oricând ca cineva să propună o soluţie valabilă la o problemă care a rămas nerezolvată 70 de ani” şi că interesul pentru probleme matematice îl ajută să se relaxeze, atunci când preocupările sale de bază, din domeniul biogerontologiei, au nevoie de o pauză.

Acest tip de problemă nu este nou. Una dintre cele mai renumite este “teoria celor patru culori”, care afirmă că este posibil, folosind doar patru culori, să se coloreze orice hartă, împărţită pe ţări sau regiuni, astfel încât două ţări învecinate să aibă întotdeauna culori distincte, situaţie care, în termenii teoriei grafurilor, ţările ar fi vârfurile, iar graniţele, segmentele care leagă vârfurile.

Problema Hadwiger-Nelson este însă diferită, deoarece nu este vorba, ca în cazul hărţilor, de un număr finit de puncte, ci de o infinitate. Pentru a ajunge la o soluţie, Grey a construit un graf cu un număr finit de noduri (1581), care necesită un anumit număr de culori, pentru a se respecta condiţia iniţială.

Descoperirea unui graf care necesită minimum cinci culori reprezintă un progres real, având în vedere timpul în care această problemă a rămas nerezolvată. Cu toate acestea, matematicienii vor să ştie dacă, pentru un graf cu mai puţine noduri, soluţia rămâne valabilă. Biogerontologul l-a provocat, în acest sens, pe matematicianul Terence Tao, de la Universitatea din California, înainte ca soluţia Grey să fie trecută în Proiectul Polymath. La puţin timp, informaticianul şi matematicianul Marijn Heule, de la Universitatea din Texas, a reuşit să construiască un graf în cinci culori şi cu numai 826 de vârfuri, rezultat pe care l-a postat deja pe Polymath.

Proiectul Polymath a fost lansat în 2009, de către matematicianul Timothy Gowers, de la Cambridge University, ca o platformă colaborativă deschisă cercetătorilor şi publicului larg, în vederea rezolvării unor probleme de matematică dificile sau ale căror soluţii nu sunt definitive.

Aubrey de Grey – o personalitate interesantă

Specializat în informatică, la Universitatea Cambridge, Aubrey de Grey şi-a îndreptat atenţia ulterior, ca autodidact, spre genetică, biologie celulară, biogerontologie, cu rezultate remarcabile. Din diversele interviuri acordate unor reviste şi posturi de televiziune de prestigiu, rezultă un mod de gândire interesant despre ceea ce înseamnă, din punctul lui de vedere, un om de ştiinţă.

“Există diferenţe semnificative– spune Grey – între creativitatea unui om de ştiinţă şi cea a unui inginer concentrat exclusiv pe probleme tehnice. Aceasta înseamnă, de exemplu, că pot să gândesc asupra unei probleme în feluri diferite şi să sjung la rezultate la fel de valabile”.

În domeniul gerontologiei, al combaterii cauzelor si efectelor îmbătrânirii, susţine omul de ştiinţă englez, există, la momentul actual, cercetări avansate, care ar putea creste semnificativ speranţa de viaţă, la nivel mondial. Este nevoie, însă, spune el, ca cei care deţin resursele financiare să fie interesaţi de un astfel de aspect şi să investească spre beneficiul oamenilor.

Începând cu anul 2005, Aubrey de Grey se ocupă de Proiectul SENS (Strategies for Engineered Negligible Senescence), care promovează strategii pentru creşterea speranţei de viaţă, pentru prevenirea declinului fizic şi mental, considerând că felul în care oamenii gândesc, în prezent, despre vârste, despre boli, despre degenerescenţă este efectul unor stereotipii transmise din generaţie în generaţie, pentru că, în realitate, organismul uman are uriaşe potenţialităţi pentru a rămâne tânăr până la vârste înaintate.

Aubrei de Grey este, de asemenea, cofondator al Methusalah Foundation (denumire care face aluzie la celebrul personaj biblic, Mathusalem, care a trăit, după cum spun textele sacre, 969 de ani). A fost instituit şi un premiu al Fundaţiei Mathusalem, în valoare de 4 milioane de dolari, pentru a încuraja cercetările care să ofere soluţii pentru ca viaţa oamenilor să fie mai bună, mai sănătoasă, mai indelungată, mai fericită.