Problema Monty Hall sau Paradoxul Monty Hall este un puzzle probabilistic, care scoate la iveală unele dintre intuițiile noastre eronate legate de probabilități. Numele provine de la gazda unui popular show TV american, “Let’s Make a Deal”, care a debutat pe micile ecrane în 1963, prezentat de Monty Hall timp de aproape 30 de ani, show care continuă să fie difuzat şi astăzi, într-un format adaptat zilelor noastre.
În esenţă, “afacerea” (Let’s Make a Deal) constă în mai multe “oferte” făcute de gazda emisiunii unuia sau mai multor membri ai publicului, numiţi “traders” (comercianţi). În cel mai simplu format, unui “trader” i se acordă un premiu sau o sumă în numerar de valoare medie, iar gazda îi oferă posibilitatea de a tranzacționa pentru un premiu necunoscut, ascuns în spatele unor uşi, unor perdele sau într-o cutie mare, aflată în studio.
Paradoxul Monty Hall – o problema de probabilitate
Steve Selvin, un statistician american, profesor emerit de biostatistică, la Universitatea din California, Berkeley, ulterior la Universitatea Johns Hopkins, din Baltimore, este cel care, în 1975, a publicat un articol, în “American Statistician”, cu titlul “A Problem în Probability”, atrăgând atenţia pentru prima dată asupra a ceea ce, mai târziu, a devenit cunoscută ca “Problema Monty Hall” şi propunând o soluţie bazată pe Teorema lui Bayes (o regulă matematică pentru inversarea probabilităților condiționate, permițându-ne să găsim probabilitatea unei cauze având în vedere efectul acesteia).
Problema Monty Hall a rămas relativ necunoscută până în 1990, când o editorialistă americană, Marilyn vos Savant (femeia cu cel mai mare coeficient de inteligență/ IQ înregistrat în Cartea Recordurilor, Guinness Book, la data respectivă), performantă în rezolvarea a diverse puzzle-uri logice, matematice sau de vocabular, a făcut cunoscută Problema Monty Hall în întreaga lume, generând dezbateri aprinse. Aceasta sublinia, de asemenea, că oamenii, în general, au mari probleme în a evalua evenimentele incerte, că se apelează, de obicei, la “reguli generale”, pentru a lua decizii mai rapid, chiar dacă acest lucru duce adesea la greșeli.
În ce constă Problema Monty Hall?
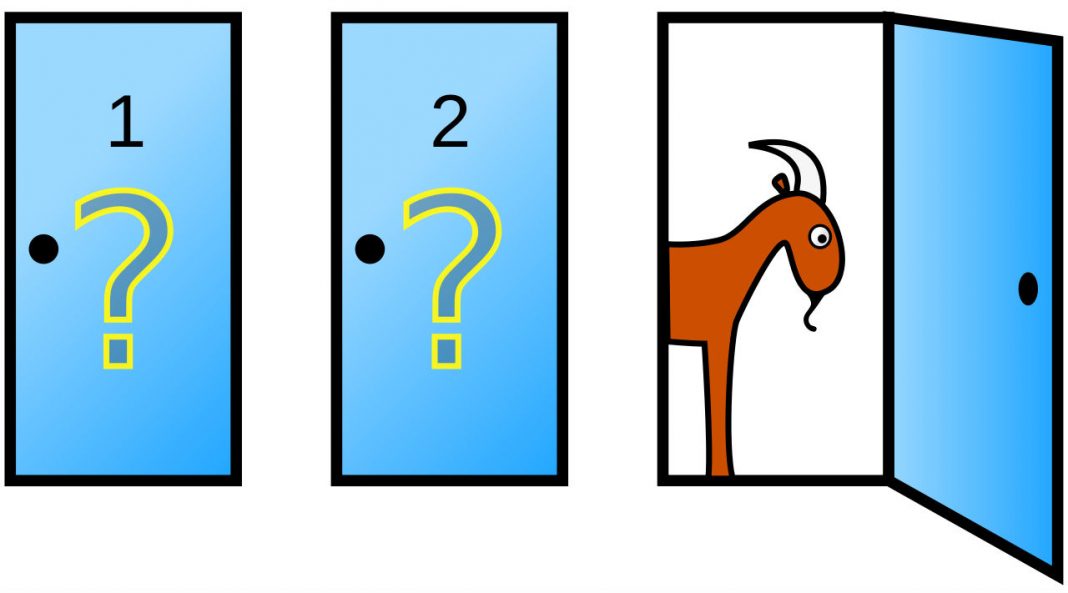
În cadrul show-ului care a generat Problema Monty Hall, prezentatorul plasa “trader”-ul (“comerciantul”) în faţa a trei uşi. În spatele uneia dintre uşi se afla premiul cel mare (de exemplu, o maşină), iar in spatele celorlalte două uşi, câte o capră (premiu, evident, nedorit). Iniţial, trader-ul alegea una dintre uşi, să spunem uşa numărul 1 (fără ca aceasta să fie deocamdată deschisă). În acest moment Monty Hall deschidea una dintre celelalte două uși, despre care el ştia că ascunde o capră şi-l întreba pe trader dacă vrea să-şi schimbe alegerea.
Cei mai mulţi competitori decideau să nu schimbe uşa, pentru că, rămânând numai două uşi, gândeau acestia, erau 50% șanse ca mașina să fie în spatele uneia sau celeilalte.
Întrebarea care se pune este: Ar trebui ca trader-ul să rămână la alegerea inițială sau să schimbe ușa?
Răspunsul și explicația pentru Problema Monty Hall
Explicaţia dată de statiscianul Steve Selvin este următoarea: deși pare că schimbarea ușii nu ar trebui să facă nicio diferență, realitatea este că ar trebui ca alegerea să fie schimbată, pentru a mări șansele de câștig. Probabilitatea de a câștiga, schimbând ușa, este de 2/3, în timp ce probabilitatea de a câștiga, rămânând la alegerea inițială, este de 1/3.
La început, alegi o ușă. Probabilitatea ca mașina să fie în spatele ușii alese de tine este de 1/3. Astfel, probabilitatea ca mașina să fie în spatele uneia dintre celelalte două uși este de 2/3. După ce Monty Hall deschide o ușă cu o capră, șansele se redistribuie, dar probabilitatea totală pentru ușile pe care nu le-ai ales rămâne la 2/3. Cum una dintre ele a fost deja exclusă, probabilitatea de 2/3 se „concentrează” pe cealaltă ușă rămasă. Dacă schimbi alegerea, vei avea șanse de 2/3 să câștigi, în timp ce, rămânând la alegerea inițială, șansele rămân 1/3.
Intuiție greșită?
Intuiția noastră ne spune că după ce o ușă este deschisă, avem două uși și ar trebui să fie şanse 50/50, dar acest lucru este greșit din cauza informațiilor suplimentare pe care Monty Hall le oferă când deschide o ușă cu o capră.
Mulţi (inclusiv matematicieni) insistă ca fiecare dintre alternativele necunoscute (în acest caz, ușile nedeschise) trebuie să aibă o probabilitate egală. Acest lucru este valabil pentru jocurile de noroc simetrice, cum ar fi fețele unei monede sau ale unui zar, și este un punct de plecare rezonabil atunci când nu se ştie absolut nimic despre alternative, dar nu este o lege a naturii, spunea Vos Savant, cea mai inteligentâ femeie din lume.
Un exemplu simplificat, care ajută la înțelegerea probabilităților, implică extinderea numărului de uși. Să presupunem că există 100 de uși. În spatele unei singure uși se află mașina, iar în spatele celorlalte 99 de uși sunt capre. Alegi inițial o ușă (probabilitatea ca mașina să fie acolo este de doar 1/100). Apoi, Monty deschide 98 de uși dintre cele rămase, toate cu capre. În acest scenariu, probabilitatea ca mașina să fie în spatele uneia dintre ușile rămase (cea pe care ai ales-o tu și cea pe care Monty nu a deschis-o) este mult mai mare pentru cealaltă ușă – aproape 99/100.
Pentru sceptici…

Pentru cei care sunt sceptici în raport cu acest raţionament, statisticienii recomandă un test simplu, cu un joc de cărţi (sau un joc online), care va demonstra că strategia constând în schimbarea alegerii iniţiale câștigă de două ori mai des decât strategia constând în păstrarea primei alegeri.
O metodă intuitivă de a înțelege Problema Monty Hall este de a încerca să o explici unui prieten, într-un joc simplu – pune un obiect mic, cum ar fi o minge, sub unul dintre trei pahare și cere-i prietenului să aleagă unul; după alegere, ridică un pahar despre care știi că nu are mingea dedesubt, întreabă-ţi prietenul dacă vrea să schimbe paharul şi, după câteva runde, observând că schimbarea conduce frecvent la câștig, devine evident că strategia este optimă.
Aceste exemple și variații arată cum “schimbarea ușii” este o alegere mai bună, chiar dacă la prima vedere pare contraintuitivă. Iluzia statistică, spun specialiştii, apare deoarece procesul creierului de evaluare a probabilităților în problema Monty Hall se bazează pe o presupunere falsă. Similar cu iluziile optice, iluzia poate părea mai reală decât răspunsul real.


















